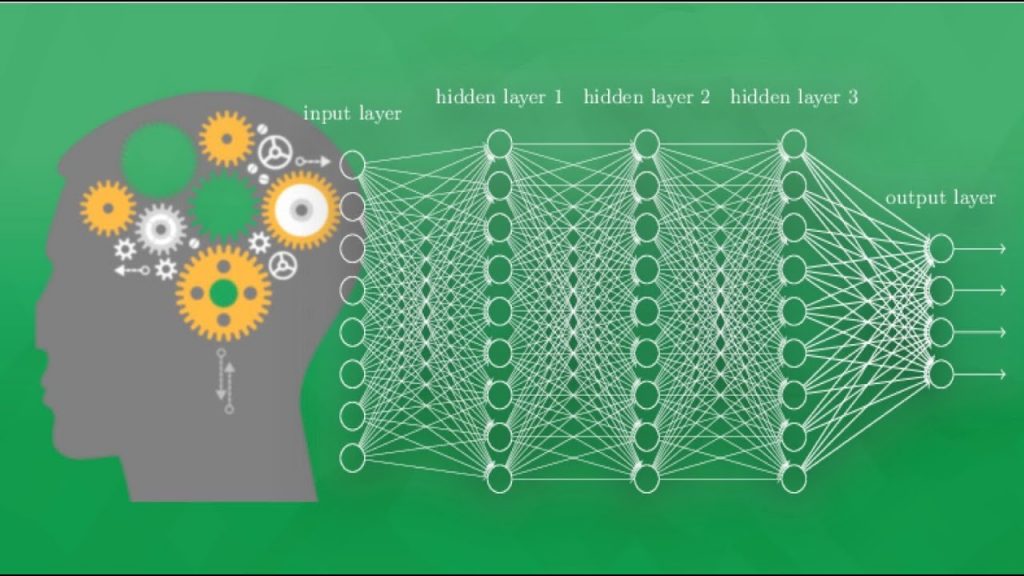
全连接神经网络模型是一种多层感知机(MLP),感知机的原理是寻找类别间最合理、最具有鲁棒性的超平面,最具代表的感知机是SVM支持向量机算法。神经网络同时借鉴了感知机和仿生学,通常来说,动物神经接受一个信号后会发送各个神经元,各个神经元接受输入后根据自身判断,激活产生输出信号后汇总从而实现对信息源实现识别、分类,一个典型的神经网络如下图所示:
上图是典型的全连接神经网络模型(DNN),有的场合也称作深度神经网络,与传统的感知机不同,每个结点和下一层所有结点都有运算关系,这就是名称中‘全连接’的含义,上图的中间层也成为隐藏层,全连接神经网络通常有多个隐藏层,增加隐藏层可以更好分离数据的特征,但过多的隐藏层也会增加训练时间以及产生过拟合。
全连接神经网络与感知机一样,仍然是利用超平面提取样本数据特征,在SVM和逻辑回归曾介绍过,感知机通过核函数将样本数据升维后可实现线性可分。观察上图,输入数据是一个3维向量,隐藏层有5个结点,意味着通过线性映射将3维向量映射为一个5维向量,最后再变为一个2维向量输出。当原输入数据是线性不可分时,全连接神经网络是通过激活函数产生出非线性输出,常见的激活函数有Sigmoid,Tanh,Relu,分别如下图所示:
全连接神经网络训练分为前向传播、后向传播两个过程,前向传播数据沿输入到输出后计算损失函数值,后向传播则是一个优化过程,利用梯度下降法减小前向传播产生的损失函数值,从而优化、更新参数,接下来详细介绍这两个过程。
一、前向传播(FP)
以一个线性回归问题为例,下图是蓝色点代表样板点,样本点大致符合线性方程y=2.3x +4.7走势,红色线标注出目标直线方程。
选择的全连接神经网络输入维度是1维,两个隐藏层,其中第一个隐藏层有2个结点,第二个隐藏层含5个结点,输出维度为1维,效果图如下:
本例是线性回归问题,选用的损失函数是平方误差函数,如果全连接神经网络用于分类,一般选择交叉熵作为损失函数。上图的神经网络经过第一次隐藏层后,一维变量转换为2维,再经过第二层隐藏层后由2维变为5维向量,如果没有激活函数引入,这两个过程是简单的线性映射过程,以结点1、2传递到结点3过程为例,用矩阵可表示该过程:
通常将x1w13+x2w23称为结点3的输入,用net3表示, net3再经过激活函数处理后变为结点3的输出,不妨用out3表示结点3的输出:
out3=σ(net3)
σ表示激活函数,本例中使用Sigmoid函数作为激活函数,在逻辑回归一篇中曾介绍过Sigmoid函数,设y=σ(x),其导数为:
σ'(x)=σ(x)(1-σ(x))=y(1-y)
激活函数可使结点产生非线性输出进而拟合复杂的曲线特征,将输入和输出结合起来,上图中结点3放大后可用下图来表示:
结点中∑代表输入,σ表示激活函数输出,有两点需要注意:
1、目前神经网络训练中已经很少使用Sigmoid函数,Sigmoid函数容易过早的梯度为0,当神经网络层数、结点增多时,这种特性易造成梯度消失,实践中大多采用Relu函数,Relu函数表示为:
Relu(x)=max{0,x}
当输入值x大于0时,Relu函数梯度始终为1。另外观察激活函数可以发现:当输入值出了某个范围之后梯度(函数斜率)变化不显著或者急剧上升,也就是产生了梯度爆炸或消失,一般将数据输入到激活函数前通过Batch Normalize做归一化处理,可有效的解决梯度爆炸或消失。
2、当网络层数变多时训练结果正确率反而下降,这可通过ResNet(残差网络)将部分层跳跃直连。
3、当结点多时,全连接神经网络很容易过拟合,Alex、Hinton在其论文《ImageNet Classification with Deep Convolutional Neural Networks》中用到了Dropout算法,用于防止接神经网络过拟合。Dropout事先设定一个概率,如设定概率为0.5,那么每个结点在前向传播时会有50%被激活,也有50%被关闭进而停止工作,Dropout本质是减少结点间相互依赖,利用取平均值的方法在训练过程中产生出一个投票策略,Dropout效果如下图:
利用pytorch演示全连接神经网络实现线性回归的过程:
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn, optim
BATCH_SIZE= 20
learning_rate = 0.02
#保存模型
savePath='model/regressmodel.pkl'
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#继承nn.Module类,自定义DNN
class Activation_Net(nn.Module):
def __init__(self, in_dim, n_hidden_1, n_hidden_2, out_dim):
super(Activation_Net, self).__init__()
self.layer1 = nn.Sequential( nn.Linear(in_dim, n_hidden_1 ), nn.Sigmoid())
self.layer2= nn.Sequential(nn.Linear(n_hidden_1, n_hidden_2), nn.Sigmoid())
self.layer3= nn.Sequential( nn.Linear(n_hidden_2, out_dim ) )
def forward(self, x):
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
return x
def loadsamples(num):
x =torch.linspace(0,3,num)
y=2.3*x +4.7 +torch.randn(1,num)
y_=2.3*x +4.7
return x,y,y_
def train():
x, y, y_=loadsamples(100)
model = Activation_Net(1,2, 5, 1)
model.train()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
epoch = 0
iternum = 200
for i in range(iternum):
for j in range(x.shape[0]):
out = model(torch.tensor([x[j].item()]))
loss = criterion(out, y_[j])
print_loss = loss.data.item()
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch += 1
if epoch % 100 == 0:
print('迭代轮: {}, 错误率: {:.4}'.format(epoch, print_loss), end='\r', flush=True)
torch.save(model, savePath)
def test():
x, y, y_ = loadsamples(100)
model = torch.load(savePath)
#测试时切换到到eval模式,取消Dropout激活功能,本例没有使用Dropout
model.eval()
x_=torch.from_numpy( np.expand_dims(x.detach().numpy(),1) )
predict = model(x_ )
p1=plt.scatter(x,y,c='cornflowerblue')
p2=plt.plot(x, y_, c='crimson',lw=2)
p3=plt.plot(x, predict.detach().numpy(), c='gold',lw=2)
plt.legend(['实际函数','神经网络', '样本'] )
plt.show()
if __name__=='__main__':
train()
#测试模型
test()
请先安装pytorch库,另外在程序目录下新建model目录用于保存模型,测试效果图如下:
黄色线代表神经网络训练出的模型,由于加入了激活函数,所以该模型具有非线性特征。
二、反向传播(BP)
反向传播根据前向传播产生的损失函数值,沿输出端向至输入端优化每层之间参数,在此过程中运算利用梯度下降法优化参数,神经网络求解参数本质上仍然是规划中求最优解问题,现代机器学习框架如Tensorflow、pytorch、keras将梯度下降法、Booting、Bagging这些优化中常用技巧封装起来,开发者只要专注于数据建模即可。
2.1 输出层权重更新
以之前代码为例,结点8为输出端,代码:
self.layer3= nn.Sequential( nn.Linear(n_hidden_2, out_dim ) )
说明结点8输出时并未使用激活函数,结点8的输入等于输出
y=net8=out8
利用链式法则,第二个隐藏层到输出结点中权重梯度为:
结合本例,此时wij的下标范围i=3,4,5,6,7 ; j=8。求损失函数最小值,则每个权重取梯度反方向则可获得优化:
公式(1)中α称为学习率,在一维搜索中曾详细介绍过,α也称为步长系数。为了后期推导方便引入输入误差概念,如输出端即结点⑻的输入误差为:
每层输入误差是对输入到该层没经过激活函数前向量求导,利用输入误差可以统一推导公式,在以后的其他神经网络中还会继续使用这个概念。另外强调一点,在目前的神经网络框架中,最终输出建议为一个实数即一个标量,如本例结点8输出的是一维标量,这样能确保反向传播时第一层误差是标量对向量、矩阵求导,如果输出时多维时,调用反向传播函数loss.backward时会把多维输出与一个向量做内积变为一个实数,向量、矩阵、标量之间求导请参考本站文章:矩阵/向量/标量间相互求导。
2.2 隐藏层之间权重更新
接下来再看两个隐藏层之间权重更新,即1,2结点与3,4,5,6,7之间权重:
self.layer2= nn.Sequential(nn.Linear(n_hidden_1, n_hidden_2), nn.Sigmoid())
两个隐藏层间输出使用了激活函数Sigmoid,以结点3输入为例:
net3=x1w13+x2w23
结点3输出为:
out3=σ(net3)
通过链式法则求两个隐藏层之间两个结点权重wij,此时下标范围i=1,2,而j=3,4,5,6,7:
上式的关键是需要求出
隐藏层之间权重更新公式为:
本例中输出端是一维的,即只有一个结点8,当输出端是多维度时
公式中
三、利用全连接神经网络识别minist数据集
上例中利用平方差作为损失函数实现了一个线性回归问题,接下来利用交叉熵作为损失函数实现对minist数据集的识别,minist数据集是手写数字的图像样本